Capsule 7: Tests statistiques

Caroline Patenaude
Bibliothécaire - Bibliothèque des lettres et sciences humaines

Script Colab | Script R

# Chargement des modules nécessaires
library(car)
library(questionr)
library(effects)

# Ajouter la fonction de téléchargement si nécessaire:
# install.packages("car", dependencies=TRUE)
# install.packages("questionr", dependencies=TRUE)
# install.packages("effects", dependencies=TRUE)

# Téléchargement de la base de données hdv2003 du module questionr
# (Extrait de l'enquête "Histoire de vie" de l'Insee - https://www.insee.fr/fr/statistiques/2532244)
data(hdv2003)

# Copie de la base de données dans un objet (datatable) nommé bd
bd <- hdv2003

1. Analyses statistiques

• On retrouve une multitude de modules dédiés aux méthodes statistiques (comme stats, MASS, FactoMineR, plm, glm).
• La même méthode peut se trouver avec variantes dans plusieurs modules.
• Les exemples ci-dessous proviennent principalement du module stats (module par défaut) où l’on retrouve de nombreuses fonctions pour différents types d’analyse.

1.1. Notation formule et objet modèle

mod <- nom.test(VD ~ VI)

• Souvent utilisé dans les modèles d’analyse (régressions…) et les graphiques.
• Peut s’interpréter comme en “fonction de…”: variable dépendante (effet) en fonction (~) de la var indépendante (cause).
• Toutes les fonctions n’acceptent pas la notation formule, mais est utilisée pour la plupart des modèles d’analyse.
• On stocke l’analyse dans un objet qui contiendra les résultats qui, selon l’analyse, inclueront un ensemble d’éléments d’information auxquels on pourra accéder de deux façons:

En passant notre objet-modèle à différentes fonctions génériques (selon le type de test):

mod <- lm(y ~ x, data=NomObjet) # Créer son objet modèle
mod                             # résumé des résultats
summary(mod)                    # ensemble des résultats détaillés
coef(mod)                       # coefficients et erreurs standards
residuals(mod)                  # résidus
confint(mod)                    # intervalles de confiance
fitted(mod)                     # valeurs ajustées
anova(mod)                      # appliquer analyse de variance sur modèle
predict(mod)                    # calculer des valeurs prédites à partir d'un modèle
plot(mod)                       # et nombreuses autres fonctions graphiques  

En utilisant la fonction names(NomObjet) et en sélectionnant individuellement le nom de l’élément avec l’opérateur $:

mod <- lm(y ~ x) # Créer son objet modèle
names(mod)       # Voir les éléments du résultat
mod$coefficients # Sélectionner l'élément individuel

À noter: par défaut les résultats sont présentés selon la notation scientifique. Pour la désactiver utiliser l’instruction: options(scipen = 999). Pour la réactiver: options(scipen = 0)

1.2. Les modalités de référence

• Dans R, il n’est pas nécessaire de recoder ses variables en “dummy”, les analyses s’en chargent par défaut lorsqu’on utilise des variables qualitatives.
• Mais attention à la modalité de référence des facteurs définie par défaut: la première dans la liste des niveaux.

# Pour voir la modalité de référence - première listée
levels(bd$sport)

## [1] "Non" "Oui"

# Pour modifier la catégorie de référence
bd$sport <- relevel(bd$sport, ref = "Oui")

2. Intervalle de confiance

# Intervalle de confiance d’une proportion

# fonction prop.test
# Calcul l'intervalle pour la première catégorie du tableau
prop.test(table(bd$sport))

## 
##  1-sample proportions test with continuity correction
## 
## data:  table(bd$sport), null probability 0.5
## X-squared = 152.9, df = 1, p-value < 0.00000000000000022
## alternative hypothesis: true p is not equal to 0.5
## 95 percent confidence interval:
##  0.3404821 0.3830553
## sample estimates:
##      p 
## 0.3615

options(scipen = 999) # désactiver la notation scientifique

# Modifier la catégorie de référence avec la fonction relevel directement dans la fonction table()
prop.test(table(relevel(bd$sport, "Oui")))

## 
##  1-sample proportions test with continuity correction
## 
## data:  table(relevel(bd$sport, "Oui")), null probability 0.5
## X-squared = 152.9, df = 1, p-value < 0.00000000000000022
## alternative hypothesis: true p is not equal to 0.5
## 95 percent confidence interval:
##  0.3404821 0.3830553
## sample estimates:
##      p 
## 0.3615

# Intervalle de confiance d'une moyenne

# Fonction t.test
# Changer le niveau de confiance avec l'argument (bd$age, conf.level=.x)
t.test(bd$age, conf.level=.99)

## 
##  One Sample t-test
## 
## data:  bd$age
## t = 127.12, df = 1999, p-value < 0.00000000000000022
## alternative hypothesis: true mean is not equal to 0
## 99 percent confidence interval:
##  47.18027 49.13373
## sample estimates:
## mean of x 
##    48.157

3. Test du Khi-carré

# Passe les variables comme argument à la fonction chisq.test() (Module questionr)

mod.chi <- chisq.test(bd$sport, bd$sexe) 

# Applique correction par défaut, sinon ajouter argument: ,correct=FALSE

mod.chi

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  bd$sport and bd$sexe
## X-squared = 16.574, df = 1, p-value = 0.00004679

# Fonction names() pour voir les éléments d'information de nos résultats
names(mod.chi)

## [1] "statistic" "parameter" "p.value"   "method"    "data.name" "observed" 
## [7] "expected"  "residuals" "stdres"

# Voir les valeurs attendues
mod.chi$expected

##         bd$sexe
## bd$sport    Homme    Femme
##      Oui 324.9885 398.0115
##      Non 574.0115 702.9885

# Fonction chisq.residuals() du module questionr pour les résidus
tab <- table(bd$sport, bd$sexe)
chisq.residuals(tab) 

##      
##       Homme Femme
##   Oui  2.44 -2.21
##   Non -1.84  1.66

4. Test de fisher

fisher.test(bd$sport, bd$sexe)

## 
##  Fisher's Exact Test for Count Data
## 
## data:  bd$sport and bd$sexe
## p-value = 0.00004629
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##  1.217630 1.772444
## sample estimates:
## odds ratio 
##   1.468833

5. Différence de moyennes entre deux groupes (Test T)

Vérifier si les moyennes d’une variable quantitative de deux groupes sont statistiquement différentes

# Explorer les statistiques descriptives selon les groupes avec la fonction by()

by(bd$age, bd$sport, FUN=summary)

## bd$sport: Oui
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   18.00   29.00   39.00   40.93   51.50   89.00 
## ------------------------------------------------------------ 
## bd$sport: Non
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   18.00   40.00   52.00   52.25   64.00   97.00

by(bd$age, bd$sport, FUN=var)

## bd$sport: Oui
## [1] 231.8337
## ------------------------------------------------------------ 
## bd$sport: Non
## [1] 272.0692

# Normalité des distributions - Test de Shapiro-Wilk

## Avec la fonction by
by(bd$age, bd$sport, FUN=shapiro.test)

## bd$sport: Oui
## 
##  Shapiro-Wilk normality test
## 
## data:  dd[x, ]
## W = 0.96203, p-value = 0.0000000000009734
## 
## ------------------------------------------------------------ 
## bd$sport: Non
## 
##  Shapiro-Wilk normality test
## 
## data:  dd[x, ]
## W = 0.98844, p-value = 0.00000001654

# Égalité des variances - test F

var.test(age ~ sport, data = bd)

## 
##  F test to compare two variances
## 
## data:  age by sport
## F = 0.85211, num df = 722, denom df = 1276, p-value = 0.01621
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.7497388 0.9707395
## sample estimates:
## ratio of variances 
##          0.8521131

# Test de Levene (module car)

leveneTest(bd$age, bd$sport) # Accepte aussi notation formule

## Levene's Test for Homogeneity of Variance (center = median)
##         Df F value   Pr(>F)   
## group    1  7.5237 0.006144 **
##       1998                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Test T 

t.test(age ~ sport, data = bd)

## 
##  Welch Two Sample t-test
## 
## data:  age by sport
## t = -15.503, df = 1600.4, p-value < 0.00000000000000022
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -12.759002  -9.893117
## sample estimates:
## mean in group Oui mean in group Non 
##          40.92531          52.25137

# Par défaut, la fonction t.test est un test de Welsh qui ne suppose pas égalité des variances

# Pour un test t classique, ajouter l'argument var.equal = TRUE

t.test(age ~ sport, data=bd, var.equal= TRUE)

## 
##  Two Sample t-test
## 
## data:  age by sport
## t = -15.164, df = 1998, p-value < 0.00000000000000022
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -12.790849  -9.861269
## sample estimates:
## mean in group Oui mean in group Non 
##          40.92531          52.25137

# Pour un test d'échantillons appariés (mesures répétées), ajouter argument paired=TRUE (sans notation formule)

6. Test Wilcoxon/Mann-Whitney (test non-paramétrique parmi d’autres)

wilcox.test(age ~ sport, data = bd)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  age by sport
## W = 282694, p-value < 0.00000000000000022
## alternative hypothesis: true location shift is not equal to 0

7. Différence de moyenne pour plus de deux groupes (ANOVA)

Évaluer la relation entre une variable quantitative et une variable qualitative avec plus de deux modalités

# Explorer les statistiques descriptives avec la fonction tapply()
# Vérifier si les moyennes semblent différentes entre les groupes
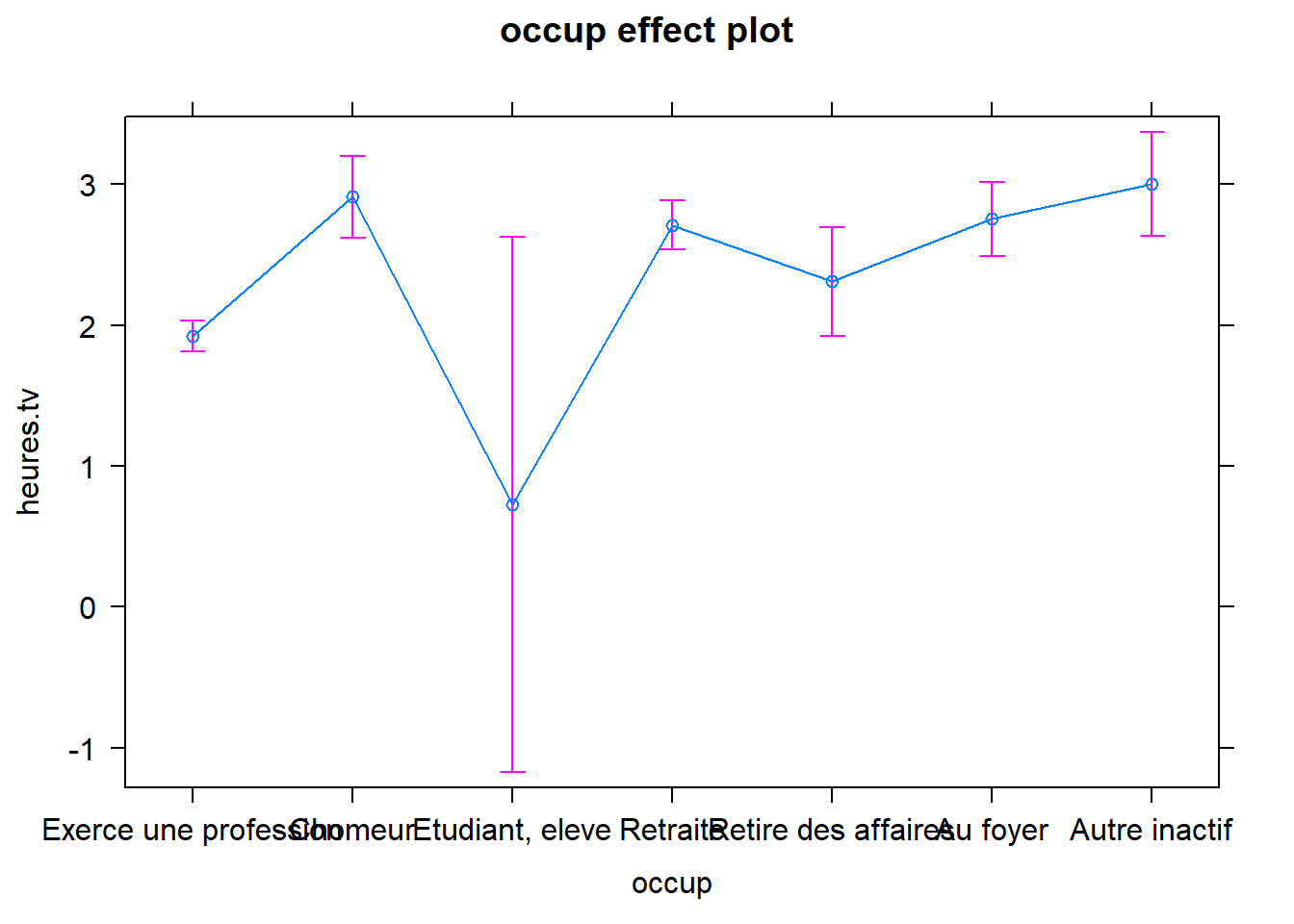
tapply(bd$heures.tv, bd$occup, mean, na.rm=T)

## Exerce une profession               Chomeur       Etudiant, eleve 
##              1.821681              2.874809              1.329787 
##              Retraite   Retire des affaires              Au foyer 
##              2.850255              2.624675              2.822222 
##         Autre inactif 
##              3.265060

# Fonction aov

mod.aov <- aov(heures.tv ~ occup, data=bd)

# Créé un objet contenant le modèle
# Pour voir effet combiné entre facteurs mod.aov <- aov(heures.tv ~ occup*sexe, bd)

mod.aov   # Voir un résumé du modèle

## Call:
##    aov(formula = heures.tv ~ occup, data = bd)
## 
## Terms:
##                    occup Residuals
## Sum of Squares   616.355  5672.029
## Deg. of Freedom        6      1988
## 
## Residual standard error: 1.689122
## Estimated effects may be unbalanced
## 5 observations deleted due to missingness

# Applique la fonction summary à l'objet modèle pour voir résultats détaillés

summary(mod.aov)

##               Df Sum Sq Mean Sq F value              Pr(>F)    
## occup          6    616  102.73   36.01 <0.0000000000000002 ***
## Residuals   1988   5672    2.85                                
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 5 observations deleted due to missingness

# Fonction lm 

mod.lm <- lm(heures.tv ~ occup, bd)

# Peut également utiliser fonction de régression linéaire pour analyse de variance
# Permet de voir les contrastes entre les différents groupes
# La modalité de référence est "Exerce une profession" (levels(bd$occup))
# Pour changer modalité de référence, utiliser la commande relevel: mod.lm <- lm(diff ~ relevel(occup, ref="Etudiant, eleve"), data=bd)
# Possède aussi un argument subset= permettant de sélectionner des modalités. Par exemple: 
# mod2.lm <- lm(heures.tv ~ occup, bd, subset = occup %in% c("Exerce une profession", "Chomeur", "Etudiant, eleve"))

# Résumé de coefficients
mod.lm 

## 
## Call:
## lm(formula = heures.tv ~ occup, data = bd)
## 
## Coefficients:
##              (Intercept)              occupChomeur      occupEtudiant, eleve  
##                   1.8217                    1.0531                   -0.4919  
##            occupRetraite  occupRetire des affaires             occupAu foyer  
##                   1.0286                    0.8030                    1.0005  
##       occupAutre inactif  
##                   1.4434

# Applique la fonction summary à l'objet modèle:
# Coefficients + Tests associés (Test t, degré de significativité)
summary(mod.lm)

## 
## Call:
## lm(formula = heures.tv ~ occup, data = bd)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.2651 -0.8748  0.1497  1.1497  8.7349 
## 
## Coefficients:
##                          Estimate Std. Error t value             Pr(>|t|)    
## (Intercept)                1.8217     0.0522  34.897 < 0.0000000000000002 ***
## occupChomeur               1.0531     0.1565   6.728    0.000000000022489 ***
## occupEtudiant, eleve      -0.4919     0.1819  -2.705               0.0069 ** 
## occupRetraite              1.0286     0.1000  10.284 < 0.0000000000000002 ***
## occupRetire des affaires   0.8030     0.1994   4.026    0.000058832091852 ***
## occupAu foyer              1.0005     0.1393   7.182    0.000000000000969 ***
## occupAutre inactif         1.4434     0.1926   7.494    0.000000000000100 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.689 on 1988 degrees of freedom
##   (5 observations deleted due to missingness)
## Multiple R-squared:  0.09801,    Adjusted R-squared:  0.09529 
## F-statistic:    36 on 6 and 1988 DF,  p-value: < 0.00000000000000022

anova(mod.lm)

## Analysis of Variance Table
## 
## Response: heures.tv
##             Df Sum Sq Mean Sq F value                Pr(>F)    
## occup        6  616.4 102.726  36.005 < 0.00000000000000022 ***
## Residuals 1988 5672.0   2.853                                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Peut aussi obtenir des résultats d'analyse de variance (somme des carrés, degré de liberté,  valeur de F...) en appliquant anova à l'objet modèle
# À noter: Les fonctions aov() et anova() retourne la somme des carrés de type I

8. Corrélations

# Fonction cor()

cor(bd$age, bd$heures.tv, use="pairwise")

## [1] 0.1776249

# Matrice de corrélations pour deux variables quanti ou plus
# pairwise: n'utiliser que les paires d'observations complètes
# pour Spearman, rajouter argument method = "spearman"
# instruction suivante si plus de deux variables: cor(bd[,c("age", "heures.tv", "freres.soeurs")], use='pairwise')

# Fonction cor.test()

cor.test(bd$age, bd$heures.tv)

## 
##  Pearson's product-moment correlation
## 
## data:  bd$age and bd$heures.tv
## t = 8.0578, df = 1993, p-value = 0.000000000000001324
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.1347898 0.2197974
## sample estimates:
##       cor 
## 0.1776249

# Ou notation formule cor.test( ~ age + heures.tv, bd)

9. Régression linéaire

Prédire la valeur d’une variable dépendante continue sur la base des valeurs de variables indépendantes

# Fonction lm()

# Quelles variables prédisent les heures de télé écoutées

mod1.lm <- lm(heures.tv ~ occup + nivetud + sexe, data=bd) 

# On stocke le résultat dans un objet modèle pour pouvoir le manipuler avec d'autres fonctions
# Pour limiter à un sous-groupe: argument ", subset=age>50"

# Passe notre objet modèle à la fonction summary pour voir 
# le tableau des coefficients et leur test de significativité
summary(mod1.lm)

## 
## Call:
## lm(formula = heures.tv ~ occup + nivetud + sexe, data = bd)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.5428 -1.0945 -0.0752  0.8701  8.5809 
## 
## Coefficients:
##                                                                        Estimate
## (Intercept)                                                             2.17632
## occupChomeur                                                            0.98936
## occupEtudiant, eleve                                                   -1.19169
## occupRetraite                                                           0.78918
## occupRetire des affaires                                                0.38809
## occupAu foyer                                                           0.83212
## occupAutre inactif                                                      1.07830
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires  0.36670
## nivetudDerniere annee d'etudes primaires                                0.24299
## nivetud1er cycle                                                       -0.07118
## nivetud2eme cycle                                                      -0.43234
## nivetudEnseignement technique ou professionnel court                   -0.10108
## nivetudEnseignement technique ou professionnel long                    -0.24726
## nivetudEnseignement superieur y compris technique superieur            -0.77476
## sexeFemme                                                              -0.07855
##                                                                        Std. Error
## (Intercept)                                                               0.28078
## occupChomeur                                                              0.15680
## occupEtudiant, eleve                                                      0.96901
## occupRetraite                                                             0.10724
## occupRetire des affaires                                                  0.20703
## occupAu foyer                                                             0.14750
## occupAutre inactif                                                        0.19833
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires    0.32344
## nivetudDerniere annee d'etudes primaires                                  0.28367
## nivetud1er cycle                                                          0.29391
## nivetud2eme cycle                                                         0.29839
## nivetudEnseignement technique ou professionnel court                      0.28322
## nivetudEnseignement technique ou professionnel long                       0.31042
## nivetudEnseignement superieur y compris technique superieur               0.28492
## sexeFemme                                                                 0.08173
##                                                                        t value
## (Intercept)                                                              7.751
## occupChomeur                                                             6.310
## occupEtudiant, eleve                                                    -1.230
## occupRetraite                                                            7.359
## occupRetire des affaires                                                 1.875
## occupAu foyer                                                            5.642
## occupAutre inactif                                                       5.437
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires   1.134
## nivetudDerniere annee d'etudes primaires                                 0.857
## nivetud1er cycle                                                        -0.242
## nivetud2eme cycle                                                       -1.449
## nivetudEnseignement technique ou professionnel court                    -0.357
## nivetudEnseignement technique ou professionnel long                     -0.797
## nivetudEnseignement superieur y compris technique superieur             -2.719
## sexeFemme                                                               -0.961
##                                                                                  Pr(>|t|)
## (Intercept)                                                            0.0000000000000149
## occupChomeur                                                           0.0000000003479586
## occupEtudiant, eleve                                                               0.2189
## occupRetraite                                                          0.0000000000002755
## occupRetire des affaires                                                           0.0610
## occupAu foyer                                                          0.0000000194364641
## occupAutre inactif                                                     0.0000000613298073
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires             0.2571
## nivetudDerniere annee d'etudes primaires                                           0.3918
## nivetud1er cycle                                                                   0.8087
## nivetud2eme cycle                                                                  0.1475
## nivetudEnseignement technique ou professionnel court                               0.7212
## nivetudEnseignement technique ou professionnel long                                0.4258
## nivetudEnseignement superieur y compris technique superieur                        0.0066
## sexeFemme                                                                          0.3367
##                                                                           
## (Intercept)                                                            ***
## occupChomeur                                                           ***
## occupEtudiant, eleve                                                      
## occupRetraite                                                          ***
## occupRetire des affaires                                               .  
## occupAu foyer                                                          ***
## occupAutre inactif                                                     ***
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires    
## nivetudDerniere annee d'etudes primaires                                  
## nivetud1er cycle                                                          
## nivetud2eme cycle                                                         
## nivetudEnseignement technique ou professionnel court                      
## nivetudEnseignement technique ou professionnel long                       
## nivetudEnseignement superieur y compris technique superieur            ** 
## sexeFemme                                                                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.673 on 1868 degrees of freedom
##   (117 observations deleted due to missingness)
## Multiple R-squared:  0.1303, Adjusted R-squared:  0.1237 
## F-statistic: 19.98 on 14 and 1868 DF,  p-value: < 0.00000000000000022

# La fonction coef présente les coefficients du modèle de régression et peut s'appliquer individuellement 
coef(mod1.lm)

##                                                            (Intercept) 
##                                                             2.17631672 
##                                                           occupChomeur 
##                                                             0.98936350 
##                                                   occupEtudiant, eleve 
##                                                            -1.19169450 
##                                                          occupRetraite 
##                                                             0.78918380 
##                                               occupRetire des affaires 
##                                                             0.38809384 
##                                                          occupAu foyer 
##                                                             0.83212236 
##                                                     occupAutre inactif 
##                                                             1.07829812 
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires 
##                                                             0.36669644 
##                               nivetudDerniere annee d'etudes primaires 
##                                                             0.24298900 
##                                                       nivetud1er cycle 
##                                                            -0.07118351 
##                                                      nivetud2eme cycle 
##                                                            -0.43234458 
##                   nivetudEnseignement technique ou professionnel court 
##                                                            -0.10107621 
##                    nivetudEnseignement technique ou professionnel long 
##                                                            -0.24725960 
##            nivetudEnseignement superieur y compris technique superieur 
##                                                            -0.77475537 
##                                                              sexeFemme 
##                                                            -0.07854815

# la fonction confint présente les intervalles de confiance (95% par défaut)
confint(mod1.lm)

##                                                                             2.5 %
## (Intercept)                                                             1.6256451
## occupChomeur                                                            0.6818472
## occupEtudiant, eleve                                                   -3.0921436
## occupRetraite                                                           0.5788704
## occupRetire des affaires                                               -0.0179321
## occupAu foyer                                                           0.5428401
## occupAutre inactif                                                      0.6893294
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires -0.2676530
## nivetudDerniere annee d'etudes primaires                               -0.3133502
## nivetud1er cycle                                                       -0.6476130
## nivetud2eme cycle                                                      -1.0175659
## nivetudEnseignement technique ou professionnel court                   -0.6565276
## nivetudEnseignement technique ou professionnel long                    -0.8560686
## nivetudEnseignement superieur y compris technique superieur            -1.3335554
## sexeFemme                                                              -0.2388450
##                                                                             97.5 %
## (Intercept)                                                             2.72698833
## occupChomeur                                                            1.29687983
## occupEtudiant, eleve                                                    0.70875456
## occupRetraite                                                           0.99949726
## occupRetire des affaires                                                0.79411978
## occupAu foyer                                                           1.12140462
## occupAutre inactif                                                      1.46726680
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires  1.00104588
## nivetudDerniere annee d'etudes primaires                                0.79932817
## nivetud1er cycle                                                        0.50524595
## nivetud2eme cycle                                                       0.15287678
## nivetudEnseignement technique ou professionnel court                    0.45437523
## nivetudEnseignement technique ou professionnel long                     0.36154943
## nivetudEnseignement superieur y compris technique superieur            -0.21595530
## sexeFemme                                                               0.08174873

# Pour le tableau ANOVA appliqué au modèle de régression
anova(mod1.lm)

## Analysis of Variance Table
## 
## Response: heures.tv
##             Df Sum Sq Mean Sq F value                Pr(>F)    
## occup        6  558.1  93.016 33.2303 < 0.00000000000000022 ***
## nivetud      7  222.5  31.780 11.3533   0.00000000000003633 ***
## sexe         1    2.6   2.585  0.9236                0.3367    
## Residuals 1868 5228.8   2.799                                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# La fonction fitted fournit les valeurs ajustées
head(fitted(mod1.lm))

##        1        3        4        5        6        7 
## 1.323013 2.419306 1.401561 3.129941 1.996692 3.172880

# La fonction resid() founit les résidus de la régression
head(resid(mod1.lm))

##            1            3            4            5            6            7 
## -1.323013191 -2.419305719  0.598438657 -0.129941371  0.003307646 -0.272879932

10. Régression logistique binaire

Prédire une variable dépendante dichotomique sur la base des valeurs de variables indépendantes

# Fonction glm
mod.reg <- glm(sport ~ sexe + nivetud + qualif, bd, family = binomial(logit))

# La fonction glm permet de calculer plusieurs modèles statistiques donc il faut indiquer à glm avec l’argument family=binomial(logit) 

# Applique fonction summary au modèle pour voir résultatsles valeurs des coefficients
summary(mod.reg)

## 
## Call:
## glm(formula = sport ~ sexe + nivetud + qualif, family = binomial(logit), 
##     data = bd)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.2994  -1.0993   0.5248   0.9188   1.4948  
## 
## Coefficients:
##                                                                        Estimate
## (Intercept)                                                             15.5105
## sexeFemme                                                                0.3809
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires -13.4420
## nivetudDerniere annee d'etudes primaires                               -13.4444
## nivetud1er cycle                                                       -14.1625
## nivetud2eme cycle                                                      -14.9886
## nivetudEnseignement technique ou professionnel court                   -14.7132
## nivetudEnseignement technique ou professionnel long                    -15.1152
## nivetudEnseignement superieur y compris technique superieur            -15.6145
## qualifOuvrier qualifie                                                  -0.1532
## qualifTechnicien                                                        -0.6169
## qualifProfession intermediaire                                          -0.5741
## qualifCadre                                                             -0.4636
## qualifEmploye                                                           -0.4086
## qualifAutre                                                              0.1229
##                                                                        Std. Error
## (Intercept)                                                              277.2085
## sexeFemme                                                                  0.1298
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires   277.2088
## nivetudDerniere annee d'etudes primaires                                 277.2085
## nivetud1er cycle                                                         277.2085
## nivetud2eme cycle                                                        277.2085
## nivetudEnseignement technique ou professionnel court                     277.2085
## nivetudEnseignement technique ou professionnel long                      277.2085
## nivetudEnseignement superieur y compris technique superieur              277.2085
## qualifOuvrier qualifie                                                     0.2463
## qualifTechnicien                                                           0.3101
## qualifProfession intermediaire                                             0.2697
## qualifCadre                                                                0.2651
## qualifEmploye                                                              0.2286
## qualifAutre                                                                0.3916
##                                                                        z value
## (Intercept)                                                              0.056
## sexeFemme                                                                2.935
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires  -0.048
## nivetudDerniere annee d'etudes primaires                                -0.048
## nivetud1er cycle                                                        -0.051
## nivetud2eme cycle                                                       -0.054
## nivetudEnseignement technique ou professionnel court                    -0.053
## nivetudEnseignement technique ou professionnel long                     -0.055
## nivetudEnseignement superieur y compris technique superieur             -0.056
## qualifOuvrier qualifie                                                  -0.622
## qualifTechnicien                                                        -1.990
## qualifProfession intermediaire                                          -2.128
## qualifCadre                                                             -1.749
## qualifEmploye                                                           -1.787
## qualifAutre                                                              0.314
##                                                                        Pr(>|z|)
## (Intercept)                                                             0.95538
## sexeFemme                                                               0.00334
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires  0.96133
## nivetudDerniere annee d'etudes primaires                                0.96132
## nivetud1er cycle                                                        0.95925
## nivetud2eme cycle                                                       0.95688
## nivetudEnseignement technique ou professionnel court                    0.95767
## nivetudEnseignement technique ou professionnel long                     0.95652
## nivetudEnseignement superieur y compris technique superieur             0.95508
## qualifOuvrier qualifie                                                  0.53390
## qualifTechnicien                                                        0.04663
## qualifProfession intermediaire                                          0.03331
## qualifCadre                                                             0.08030
## qualifEmploye                                                           0.07393
## qualifAutre                                                             0.75369
##                                                                          
## (Intercept)                                                              
## sexeFemme                                                              **
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires   
## nivetudDerniere annee d'etudes primaires                                 
## nivetud1er cycle                                                         
## nivetud2eme cycle                                                        
## nivetudEnseignement technique ou professionnel court                     
## nivetudEnseignement technique ou professionnel long                      
## nivetudEnseignement superieur y compris technique superieur              
## qualifOuvrier qualifie                                                   
## qualifTechnicien                                                       * 
## qualifProfession intermediaire                                         * 
## qualifCadre                                                            . 
## qualifEmploye                                                          . 
## qualifAutre                                                              
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 2107.1  on 1627  degrees of freedom
## Residual deviance: 1857.0  on 1613  degrees of freedom
##   (372 observations deleted due to missingness)
## AIC: 1887
## 
## Number of Fisher Scoring iterations: 14

# La fonction coef permet aussi d'obtenir les coefficients individuellement
coef(mod.reg)[1]

## (Intercept) 
##    15.51047

# La fonction exp pour les odds ratio et leurs intervalles de confiance
exp(coef(mod.reg))

##                                                            (Intercept) 
##                                                  5446419.8378982935101 
##                                                              sexeFemme 
##                                                        1.4636734332397 
## nivetudA arrete ses etudes, avant la derniere annee d'etudes primaires 
##                                                        0.0000014527840 
##                               nivetudDerniere annee d'etudes primaires 
##                                                        0.0000014493674 
##                                                       nivetud1er cycle 
##                                                        0.0000007068312 
##                                                      nivetud2eme cycle 
##                                                        0.0000003094143 
##                   nivetudEnseignement technique ou professionnel court 
##                                                        0.0000004075176 
##                    nivetudEnseignement technique ou professionnel long 
##                                                        0.0000002726146 
##            nivetudEnseignement superieur y compris technique superieur 
##                                                        0.0000001654703 
##                                                 qualifOuvrier qualifie 
##                                                        0.8579696688054 
##                                                       qualifTechnicien 
##                                                        0.5395994094327 
##                                         qualifProfession intermediaire 
##                                                        0.5632193440074 
##                                                            qualifCadre 
##                                                        0.6290228726288 
##                                                          qualifEmploye 
##                                                        0.6645837426705 
##                                                            qualifAutre 
##                                                        1.1307466368239

# Aussi la fonction odds.ratio(mod.reg) du module questionr

11. Visualiser les résultats d’un modèle

# Résultat de l'ANOVA
plot(allEffects(mod.aov))

# Résultat de la régression linéaire - effet de tous les prédicteurs

plot(allEffects(mod1.lm))

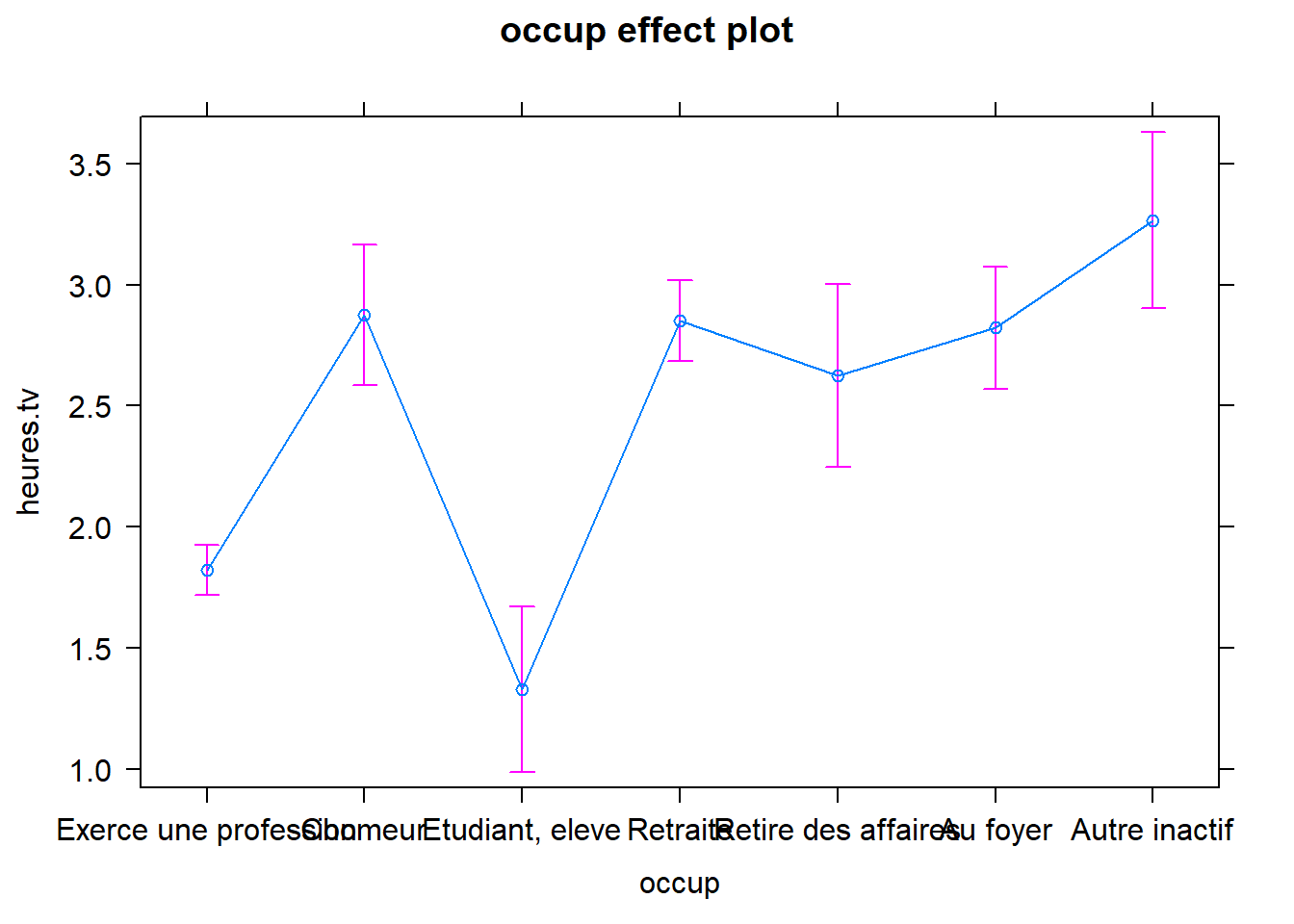
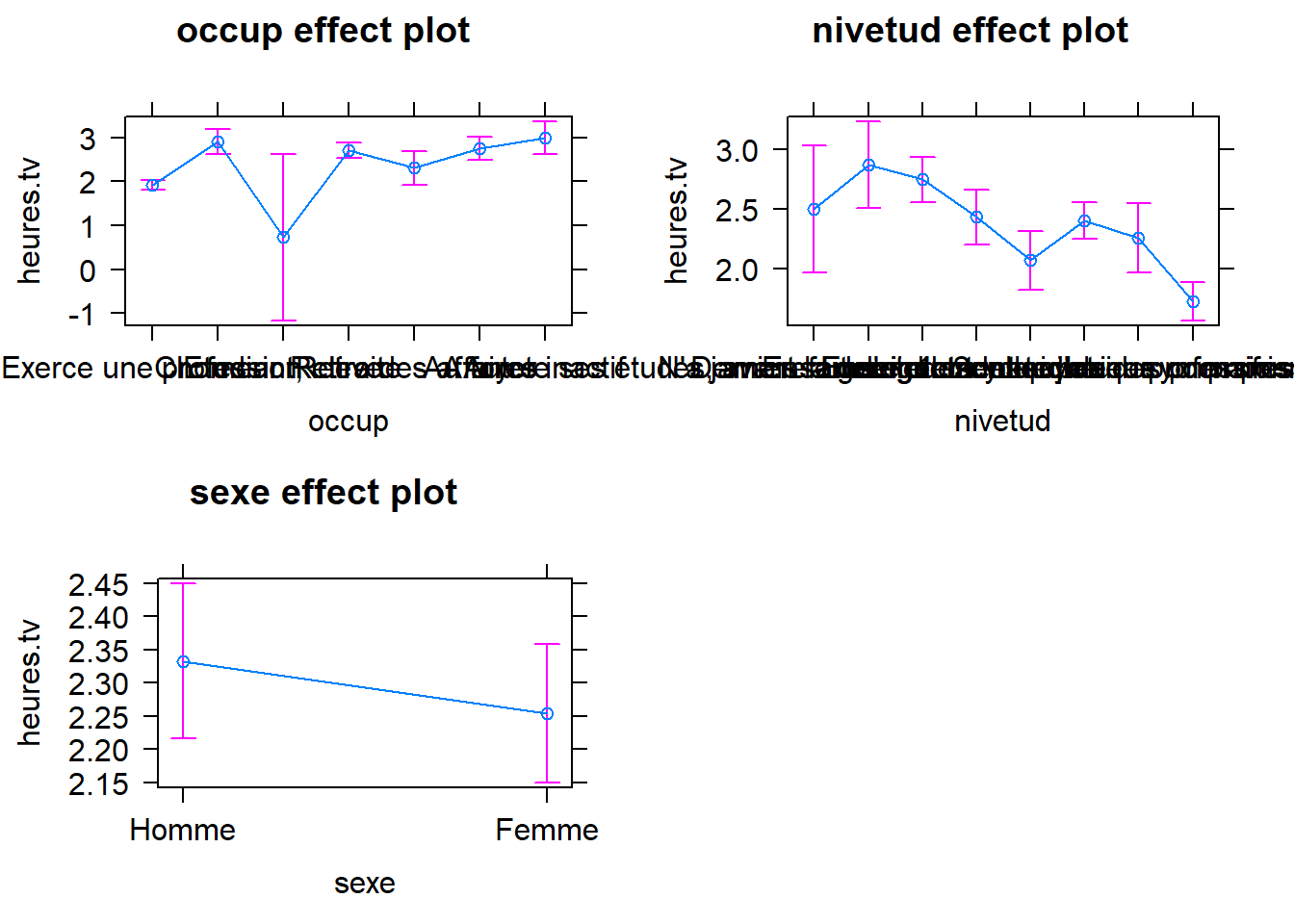
# Résultat de la régression linéaire - effet d'un seul prédicteur

plot(Effect("occup", mod=mod1.lm))

---